In the course TF ROS 101, we are trying to get one robot to follow another based on the TF readings.
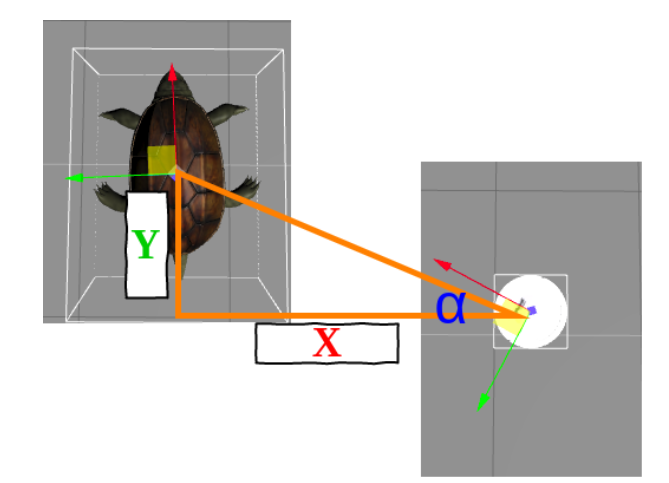
1.Can someone explain these two-line of math that is used to calculate the path and why we multiply the angle we derived by 4 in the following line:
angular = 4 * math.atan2(trans[1], trans[0])
linear = 0.5 * math.sqrt(trans[0] ** 2 + trans[1] ** 2)
2.Also I see that in both the robots the X axis is at the front and Y axis at the side , is this standard practise?
3.How would the triangle and angle look like if the iRobot (now on lower right) was at the upper right?
The complete code is as follows:
#!/usr/bin/env python
import sys
import rospy
import math
import tf
import geometry_msgs.msg
if __name__ == '__main__':
rospy.init_node('tf_listener_turtle')
listener = tf.TransformListener()
if len(sys.argv) < 3:
print("usage: turtle_tf_listener.py follower_model_name model_to_be_followed_name")
else:
follower_model_name = sys.argv[1]
model_to_be_followed_name = sys.argv[2]
turtle_vel = rospy.Publisher(follower_model_name+'/cmd_vel', geometry_msgs.msg.Twist,queue_size=1)
rate = rospy.Rate(10.0)
ctrl_c = False
follower_model_frame = "/"+follower_model_name
model_to_be_followed_frame = "/"+model_to_be_followed_name
def shutdownhook():
# works better than the rospy.is_shut_down()
global ctrl_c
print "shutdown time! Stop the robot"
cmd = geometry_msgs.msg.Twist()
cmd.linear.x = 0.0
cmd.angular.z = 0.0
turtle_vel.publish(cmd)
ctrl_c = True
rospy.on_shutdown(shutdownhook)
while not ctrl_c:
try:
(trans,rot) = listener.lookupTransform(follower_model_frame, model_to_be_followed_frame, rospy.Time(0))
except (tf.LookupException, tf.ConnectivityException, tf.ExtrapolationException):
continue
angular = 4 * math.atan2(trans[1], trans[0])
linear = 0.5 * math.sqrt(trans[0] ** 2 + trans[1] ** 2)
cmd = geometry_msgs.msg.Twist()
cmd.linear.x = linear
cmd.angular.z = angular
turtle_vel.publish(cmd)
rate.sleep()
1.Can someone explain these two-line of math that is used to calculate the path and why we multiply the angle we derived by 4 in the following line
Those values are just to define a speed for the cmd_vel. Its more related to the simulator than anything else.
Also I see that in both the robots the X axis is at the front and Y axis at the side , is this standard practise?
Yes. Thats the normal way of doing it in robotics, although you will find manufacturers not following that standard.
How would the triangle and angle look like if the iRobot (now on lower right) was at the upper right?
The same way but the triangle fliped horizonatlly.
@duckfrost2 Thanks for the quick reply. Could you explain why we multiply by 4 in little more details? the linear part is achieved by Pythagoras, but the angular part (mentioned below) is bit confusing
Could you also explain the below math in moving_extra_frame_pub.py of TF ROS 101? It would be great if the math was also explained in the course
t = (rospy.Time.now().to_sec() * math.pi)*turning_speed_rate
# Map to only one turn maximum [0,2*pi)
rad_var = t % (2*math.pi)
Full code:
#!/usr/bin/env python
import rospy
import tf
import math
if __name__ == '__main__':
rospy.init_node('my_moving_carrot_tf_broadcaster')
br = tf.TransformBroadcaster()
rate = rospy.Rate(5.0)
turning_speed_rate = 0.1
while not rospy.is_shutdown():
t = (rospy.Time.now().to_sec() * math.pi)*turning_speed_rate
# Map to only one turn maximum [0,2*pi)
rad_var = t % (2*math.pi)
br.sendTransform((1.0 * math.sin(rad_var), 1.0 * math.cos(rad_var), 0.0),
(0.0, 0.0, 0.0, 1.0),
rospy.Time.now(),
"moving_carrot",
"turtle2")
rate.sleep()
Hi,
Thats just getting the x and y components based on the angle ( thats why we use sin and cos ). Its trignometry basics ( https://www.khanacademy.org/math/geometry/hs-geo-trig/hs-geo-trig-ratios-intro/a/finding-trig-ratios-in-right-triangles )
@duckfrost2 , Thank you for the quick reply.
Thats just getting the x and y components based on the angle ( thats why we use sin and cos ). Its trignometry basics
I got the angle, but why are we multiplying the angle we got by trignomoetry by 4?
angular = 4 * math.atan2(trans[1], trans[0])
linear = 0.5 * math.sqrt(trans[0] ** 2 + trans[1] ** 2)
@duckfrost2 , Is it safe to say that we are multiplying by 4 because the values outputed from
math.atan2(trans[1], trans[0] is small and hence we are multiplying by 4 to increase the value, hence making faster turns.
@duckfrost2 @bayodesegun @albertoezquerro
I am familiar with how sin and cos works. based on my understanding, we are feeding the rad_var values into sin and cos, so that i moves along a path as below:

Can you explain how the below lines of code works?
t = (rospy.Time.now().to_sec() * math.pi) * turning_speed_rate
# Map to only one turn maximum [0,2pi)
rad_var = t % (2math.pi)
- turning_speed_rate = to set the turning speed
- rospy.Time.now().to_sec() = to get a continuos stream of values in the equation
- what is purpose for math.pi in t = (rospy.Time.now().to_sec() * math.pi) * turning_speed_rate and *rad_var = t % (2 *math.pi)
- What exactly happens in rad_var = t % (2*math.pi)
Hi,
This is just a way ( you could do it many other ways ) to generate numbers between 0-2*pi, based on the time passing by. That way we have an incremental coherent value of angles for the turning frame. As I said this could be done in loads of ways different. Just that using the time variable allows it to generate increments based on the passing of the internal clock of the simulation, which avoids jumps and similar issues.
Can you give me more info on what Jump errors are?
Jumps errors I mean that if for example your pc is not powerful enough and the simulation for whatever reason goes slow, if we don’t use the clock , we might generate values beyond what the simulation can process and might produce small jumps of values and strange movements