The right presentation of the if statement

Course Support C++ For Robotics
1

Hi support,
about the loops unit, I believe there is a mistake in the problem presentation:
I read:

if the position is greater than x limit is true then stop moving else move backwords

I think that, even in the logic of while loop, the right sentence has the opposite logic, namely:

if the position is greater than x limit is true then move backwords else stop moving

Please, let me know.

thanks
best
Salvatore

2

Hi Salvatore,

I don’t think there’s a mistake in the problem presentation. What I see, however, is a possible confusion with the implementation as it seems to be the opposite of the problem. But it’s not, because there could be two or more ways to say the same thing.

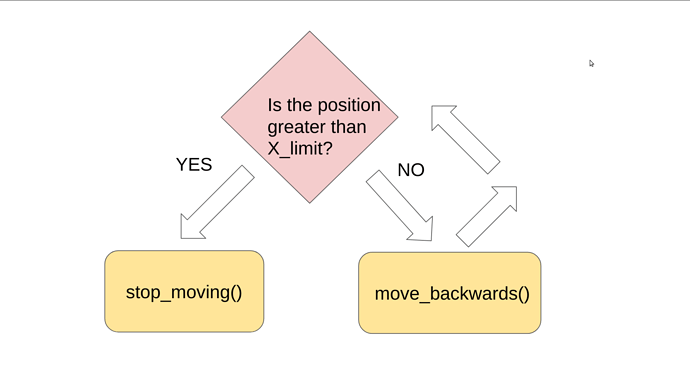
Here is the problem statement:

image
image1920×1080 117 KB

Now if we wanted to implement this verbatim, we would write:

if (postion_is_greater_than_x_limit) {
    stop_moving();
}
move_backwards();

But this would not work. Let’s assume that at the beginning x_limit is 10 and position is 1, then the loop would be skipped and the robot would move backwards ONCE and would NEVER STOP, because it will not go back to check the the loop condition again even when position gets to 11 (as the program flows from top to bottom).

What we want is for the robot to keep moving backwards while position is 10 or less, so we need to do the backward movement inside the loop. Then when that condition is no longer true, we break out of the loop and stop the robot. Which is why we introduce the opposite of the problem as the loop condition, and also reverse the actions:

if (postion_is_NOT_greater_than_x_limit) {
    move_backwards();
}
stop_moving();

So now, as position progresses from 1 through 10, the loop keeps executing and moving the robot backwards. The moment it exceeds 10, the loop breaks and we stop the robot.

We could also implement it like this:

if (postion_is_less_than_or_equal_to_x_limit) {
    move_backwards();
}
stop_moving();

Well, we could also change the problem statement so that it sounds exactly like the implementation, but that would be unrealistic because we normally don’t decide what the problem says, but we can determine how to interpret and solve it.

3

hello bay,
Thank you for your answer. I understand what you explained. What happens is that if the robot does not pass Xlimit then it proceeds backwards but, if I’m not mistaken, the robot comes back without ever stopping, right?
This is why I thought there was an error in the presentation of the problem.
Best
Salvatore

4

I understand, and in fact almost mentioned it - a critical piece of information left out of the picture:

The position is updated/increased every time the robot moves. There should be some logic in move_backwards() or elsewhere that updates position so that it eventually gets past xlimit. Also, it might seem that moving backwards takes the robot further away from xlimit, but it is not necessarily so.