Policy evaluation algorithm is different from what is explain

Course Support Reinforcement Learning for Robotics
1

Hello,

You said that in the policy evaluation you compute the sum of all values state to know if evaluation is converging to optimal values states.
But in the algorithm you compare only the maximum of the value state at each iteration, not the sum :
( if np.max(np.abs(prev_V - V)) < theta:)

Is it equivalent ? Thanks !


> def policy_evaluation(pi, P, gamma=0.99, theta=1e-10):
>     # init to random - here zeros
>     prev_V = np.zeros(len(P), dtype=np.float64)
>     while True:
>         V = np.zeros(len(P), dtype=np.float64)
>         for s in range(len(P)):
>             for prob, next_state, reward, done in P[s][pi(s)]:
>                 # sum all environmental state value
>                 V[s] += prob * (reward + gamma * prev_V[next_state] * (not done))
>         # compare if computed value state with previous value. Brake if the difference is under the threshold
>         if np.max(np.abs(prev_V - V)) < theta:
>             break
>         prev_V = V.copy()
>     return V
2

Hello @Alexbou ,

Let me share here the answer provided directly by the creator of this course (Markus Buchholz):

Let’s start with the explanation of the policy evaluation algorithm:

“The policy evaluation algorithm estimates the state - value function computed for a random policy (the strategy the agent follows). We refer to the type of algorithm that takes in a policy as input and outputs a value function. Normally in policy iteration (here policy evaluation) we start with the random policy (here we initialize to zeros), then we find the value - state function of that policy (we sum the value for each state of the environment). If the value function is not optimal then we find the new improved policy. We repeat this process until we find the optimal policy (a policy that for every state the agent can obtain expected returns greater than or equal to any other policy).”

And an image to illustrate this:
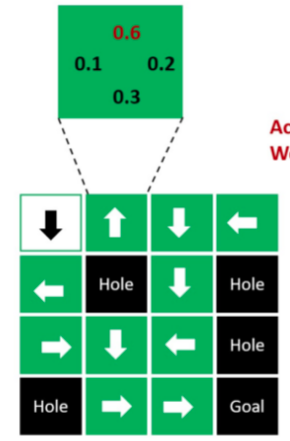
policy_evaluation

For a better understanding, Markus has created a simplified Python script with working “pseudo-code” explanation:

# The Construct 2022

import numpy as np
import random

states = 9  # environment 3x3 Maze
next_state = 4  # agent can go : up, down, left, right

V_prev = np.zeros(states)
V = np.zeros(states)

for ii in range(states):
    for jj in range(next_state):
        r = random.randint(1, 10)
        V_prev[ii] += jj + r

for ii in range(states):
    for jj in range(next_state):
        r = random.randint(1, 10)
        V[ii] += jj + r

print("V_prev : ", V_prev)
print("V : ", V)

abs_diff = np.abs(V_prev - V)
print("abs_diff : ", abs_diff)

print("max abs_diff : ", np.max(abs_diff))  # this value is compared to theta

#-----------------------------------------------------#
# similar output to be expected
# V_prev :  [25. 27. 22. 22. 34. 28. 33. 21. 37.]
# V :  [20. 23. 28. 31. 36. 34. 27. 27. 21.]
# abs_diff :  [ 5.  4.  6.  9.  2.  6.  6.  6. 16.]
# max abs_diff :  16.0
#-----------------------------------------------------#

First, a NumPy array is initiated with ZEROS and later filled with values = > for each state (for example agent is in cell 10) and can go UP, DOWN, LEFT, or RIGHT. So for all these 4 possibilities the value V[s] is computed.

Afterwards we check the difference [V - V_prev] (we compare each state separately):

[10 , 9 , 8] - [1, 2, 3] = [9, 7, 5 ]

Later we evaluate the max value (here 9) of the difference and compare again with theta: 9 < theta - see code (with other numbers).

Going back to the original code, here is where we are computing the sum for each state:

V[s] += prob * (reward + gamma * prev_V[next_state] * (not done))

And after the for loop is exhausted, we compare (against threshold) the sums: actual and previous.

if np.max(np.abs(prev_V - V)) < theta:

Hope this helps to clarify your doubts.