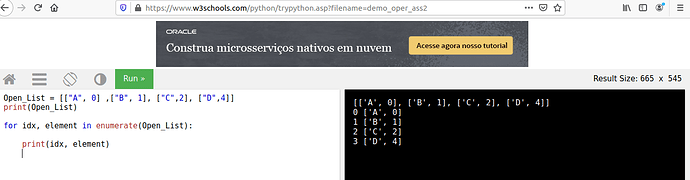
Hi I would like an assistance to upgrade my programming language knowledge 
I do not with to spend the time of experts on this doubt because they have already posted the solution.
However I have done a different code for Djikstra algorithm. And I would like to fix it to work…
But at first I really would like to understand the logic determine where a neighbour is (left, right, upper, etc) that was applied in the code below the function “find_neighbours” :
upper = index - width
if upper > 0: # What is the logic here to be upper than 0 ?
if costmap[upper] < lethal_cost:
step_cost = orthogonal_step_cost + costmap[upper]/255 # What is the logic here to divide the number 255?
neighbors.append([upper, step_cost])
left = index - 1
if left % width > 0:
if costmap[left] < lethal_cost:
step_cost = orthogonal_step_cost + costmap[left]/255
neighbors.append([left, step_cost])
upper_left = index - width - 1
if upper_left > 0 and upper_left % width > 0:
if costmap[upper_left] < lethal_cost:
step_cost = diagonal_step_cost + costmap[upper_left]/255
neighbors.append([index - width - 1, step_cost])
upper_right = index - width + 1
if upper_right > 0 and (upper_right) % width != (width - 1):
if costmap[upper_right] < lethal_cost:
step_cost = diagonal_step_cost + costmap[upper_right]/255
neighbors.append([upper_right, step_cost])
right = index + 1
if right % width != (width + 1):
if costmap[right] < lethal_cost:
step_cost = orthogonal_step_cost + costmap[right]/255
neighbors.append([right, step_cost])
lower_left = index + width - 1
if lower_left < height * width and lower_left % width != 0:
if costmap[lower_left] < lethal_cost:
step_cost = diagonal_step_cost + costmap[lower_left]/255
neighbors.append([lower_left, step_cost])
lower = index + width
if lower <= height * width:
if costmap[lower] < lethal_cost:
step_cost = orthogonal_step_cost + costmap[lower]/255
neighbors.append([lower, step_cost])
lower_right = index + width + 1
if (lower_right) <= height * width and lower_right % width != (width - 1):
if costmap[lower_right] < lethal_cost:
step_cost = diagonal_step_cost + costmap[lower_right]/255
neighbors.append([lower_right, step_cost])
There are a lot of addition, subtraction, division, index and width comparisons, that made me confuse. Could you please provide a youtube video (it does need to be from RIA) of this explanation?
After this step I am going now to try understand the errors of my code compared to the solution To get my code fixed:
Comparing my algorith to the solution, my doubts are:
- Unpack the node_index and step_cost
1- Solution code:
# Get neighbors of current_node
neighbors = find_neighbors(current_node, width, height, costmap, resolution)
# Loop neighbors
for neighbor_index, step_cost in neighbors:
# Check if the neighbor has already been visited
if neighbor_index in closed_list:
continue
1- My code:
neighbours = find_neighbors(current_node, width, height, costmap, resolution) # I forgot to add the args previously,
#without args the fucntion will not work, once it is necessary to know “who/where” the current_node is to get neighbors, as well as the grid size allowed to visit/expand
#Task 3 - The loop needs to be inner the other loop to get different g_cost values for the new current_node values, as the open_list is swept
#Invoke a loop over all elements in neighbours
neighbours_iterator = iter(neighbours) # Created this to have the possibility to skip a specific neighbour index of a list as required below
for element in neighbours_iterator:
#Unpack each neighbor into neighbor_index and step_cost for later use
neighbor_index = element[0]
step_cost = element[1]
#Check if neighbor_index is in closed_list, and if so, skip the current loop iteration and proceed with the next neighbour
if neighbor_index in closed_list:
neighbours_iterator.next() # is it necessary ? or just continue will work
continue # I am not sure if this will work or is needed another statement,
I thought this would work as the solution code…however I am not sure if the cmd "neighbours_iterator.next() is needed to visit the next neighbour of the list or just continue will do this, I mean it will jump from A to B in a list inside the for loop if A be already a visited spot on list [ A, B, C, etc]. Is this redundant? I am not sure if it is because of 2 jumps reason that my code crashes?
Keeping on the code solution to track if the neighbour is already inside open_list or not and if yes update the cost to this neighbour if be cheaper, or append the new neighbour and cost if do not be in open list. The solution used a False/True state pre-condition for later entry in if statement again:
1- Solution
# Check if the neighbor is in open_list
in_open_list = False
for idx, element in enumerate(open_list):
if element[0] == neighbor_index:
in_open_list = True
break
# CASE 1: neighbor already in open_list
if in_open_list:
if g_cost < g_costs[neighbor_index]:
# Update the node's g_cost inside g_costs
g_costs[neighbor_index] = g_cost
parents[neighbor_index] = current_node
# Update the node's g_cost inside open_list
open_list[idx] = [neighbor_index, g_cost]
# CASE 2: neighbor not in open_list
else:
# Set the node's g_cost inside g_costs
g_costs[neighbor_index] = g_cost
parents[neighbor_index] = current_node
# Add neighbor to open_list
open_list.append([neighbor_index, g_cost])
# Optional: visualize frontier
grid_viz.set_color(neighbor_index,'orange')
rospy.loginfo('Dijkstra: Done traversing nodes in open_list')
In my code, I did not use this previous check condition. But checked directly if the neighbour was in open list (with if) or not (else). For that at first I have done what the exercise asked: “unpack the variable into neighbor and cost”. In my just extracted from the variable element (that iterates over neighbour), its index and value accessing the node_index [0] and step_cost[1]. From solution what I realize is that was needed not just the node_index[0] and step_cost[1], but besides the index of both??? why. The image below display what was done on solution code:
Going back to my code I did not create and index with enumerate, but instead just got the node_index and step_cost.
2- My code:
if neighbor_index in open_list:
# Case 1:if the neighbor is already inside open_list: Verify that g_cost is better than the neighbor's current g_cost value, if so:
neighbor_new_cost = g_cost
neighbor_current_cost_open_list = [sub[neighbor_index] for sub in open_list]
# If so Update the node's g_cost inside g_costs
if neighbor_new_cost < neighbor_current_cost_open_list:
g_costs.update({neighbor_index:neighbor_new_cost})
#Modify its parent node, set it to current_node
parents.update({neighbor_index:current_node}) # It is the same as the else statement? Strange...
#Update the node's g_cost inside open_list
open_list.clear() # It is not necessary once the value of key updated above in dictionary will automatically update the list too
open_list.append(g_costs)
#Case 2, if the neighbor is not part of open_list: # It is not said but I believe it must be added not just the neighbor but also its value as well, then I will use "element" that contains both
else:
#Set the node's g_cost inside g_costs
g_costs.append({neighbor_index:g_cost}) # There is not verification as previously, you need just the step to add
#Set current_node as its parent node
parents.update({neighbor_index:current_node}) # Using update will let the first neighbor and its corresponding parent
#at the end of the parents_dictionary after finish the search, that is why it is needed to reverse the order later.
#Another issue that I realize now, is that the for loop needs to be inside the while loop, otherwise the "current_node" will always be the same.
#This is critical code considering it will have a lot of loops inside another and will become too slow, I believe
#Add the neighbor into open_list
open_list.append(element)
#Optional: add this line of code to visualize the frontier:
grid_viz.set_color(neighbor_index,'orange')
At first to
From my code, in case the neighbour be in open_list I just updated the g_costs list of dictionaries with the new value (if cheaper then previous) and afterwards, the only programming way I have found to update the g_cost on open_list, was to clear this list totally and then build it again appending the g_costs inside it. Is this right? Or if I do this I am deleting some useful value that I should not? Because on my mind I think that all the values I deleted I am going to replace, right?
What I see it is different is the addition of neighbor_index and g_cost on the last “idx” of the open_list array:
What I see it is different is the addition of the neighbor_index and g_cost at the end of my open_list array (once it gets the last value of this list, after exit the previous for loop)
open_list[idx] = [neighbor_index, g_cost] (solution)
open_list.clear()
open_list.append(g_costs) (my_code)
As I do not have an idx variable the code above should do the same?
Going to my else condition ( the neighbour is not already inside open_list), I did different from solution using just “element” variable to iterate over the neighbours list. I believe it is already enough, considering the element will get the sublist pair [node_index, step_cost] from the list neighbour. That is why wehn I use “open_list.append”, I am adding both node and its cost.
Finally going to last task of the algorithm:
Get the shortest_path.
From solution:
-
solution:
if not path_found:
rospy.logwarn('Dijkstra: No path found!') return shortest_pathReconstruct path by working backwards from target
if path_found:
node = goal_index shortest_path.append(goal_index) while node != start_index: shortest_path.append(node) # get next node node = parents[node]reverse list
shortest_path = shortest_path[::-1]
rospy.loginfo(‘Dijkstra: Done reconstructing path’)
return shortest_path
What I did not understood is how the node variable is updated just getting it from the parents dictionary inside this while loop. Because from my intuition the node=parents[node] will get just the first or last value of parents dict, once the node is not being iterated over the parents dictionary. It sounds like a magic happened here. But I cannot see.
In my point of view, I should do a for loop inside this while, to sweep the node inside the parents dictionary. I know a lot of loops inside another ones are not interesting. But is not possible to do this using a lambda function using a for loop inside brackets?
In the code below I have put in comment the for loop I have created after see the solution.
-
My code:
if closed_list[-1] != goal_index:rospy.logwarn( 'Djikstra: No path found!')else:
node = goal_index # Declare a variable named node and assign the target node to it#Enter a loop that keeps going until ‘node’ is equal to start_index
while node != start_index: #At each iteration step: #for node in parents: # while node != start_index: # Append node to shortest_path # shortest_path.append(node) # Get the next node by re-assigning node to be the node's parent node shortest_path.append(node) # Copy from solution below, however I do not understand how the node iterates over the parents dictionarywithou a for loop over parents. How does it go to next node?
node = parents[node] shortest_path.reverse() #Once the loop exits, reverse shortest_path to get the correct order ropsy.loginfo('Dijkstra: Done reconstructing path')return shortest_path
The reverse() function I used works to put list in inverse order as the solution used [:-1]?
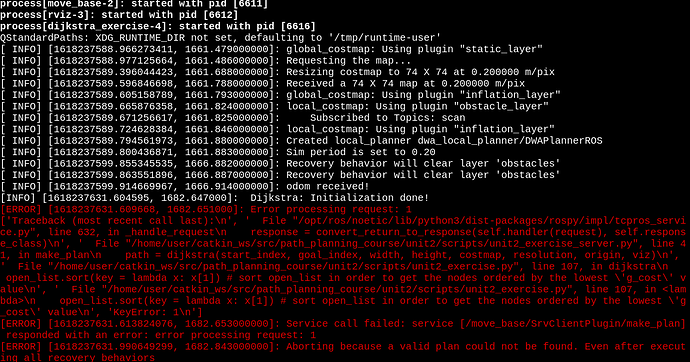
Finally I wish to understand where exactly is the beginning or the crucial points my code fails and return the error ouput below, when I try to set a goal pose in rviz:
Could you help me fix my code in order to work properly? You can access it on my account right? you can change the code there if you wish and put explanations
catkins/ws/src/path_planning/unit2/scripts/unit2_exercise.py
Anyway I will attach the code here:
#! /usr/bin/env python
"""
Dijkstra's algorithm path planning exercise
Author: Roberto Zegers R.
Copyright: Copyright (c) 2020, Roberto Zegers R.
License: BSD-3-Clause
Date: Nov 30, 2020
Usage: roslaunch unit2 unit2_exercise.launch
"""
import rospy
def find_neighbors(index, width, height, costmap, orthogonal_step_cost):
"""
Identifies neighbor nodes inspecting the 8 adjacent neighbors
Checks if neighbor is inside the map boundaries and if is not an obstacle according to a threshold
Returns a list with valid neighbour nodes as [index, step_cost] pairs
"""
neighbors = []
# length of diagonal = length of one side by the square root of 2 (1.41421)
diagonal_step_cost = orthogonal_step_cost * 1.41421
# threshold value used to reject neighbor nodes as they are considered as obstacles [1-254]
lethal_cost = 1
upper = index - width
if upper > 0: # What is the logic here to be upper than 0 ?
if costmap[upper] < lethal_cost:
step_cost = orthogonal_step_cost + costmap[upper]/255 # What is the logic here to divide the number 255?
neighbors.append([upper, step_cost])
left = index - 1
if left % width > 0:
if costmap[left] < lethal_cost:
step_cost = orthogonal_step_cost + costmap[left]/255
neighbors.append([left, step_cost])
upper_left = index - width - 1
if upper_left > 0 and upper_left % width > 0:
if costmap[upper_left] < lethal_cost:
step_cost = diagonal_step_cost + costmap[upper_left]/255
neighbors.append([index - width - 1, step_cost])
upper_right = index - width + 1
if upper_right > 0 and (upper_right) % width != (width - 1):
if costmap[upper_right] < lethal_cost:
step_cost = diagonal_step_cost + costmap[upper_right]/255
neighbors.append([upper_right, step_cost])
right = index + 1
if right % width != (width + 1):
if costmap[right] < lethal_cost:
step_cost = orthogonal_step_cost + costmap[right]/255
neighbors.append([right, step_cost])
lower_left = index + width - 1
if lower_left < height * width and lower_left % width != 0:
if costmap[lower_left] < lethal_cost:
step_cost = diagonal_step_cost + costmap[lower_left]/255
neighbors.append([lower_left, step_cost])
lower = index + width
if lower <= height * width:
if costmap[lower] < lethal_cost:
step_cost = orthogonal_step_cost + costmap[lower]/255
neighbors.append([lower, step_cost])
lower_right = index + width + 1
if (lower_right) <= height * width and lower_right % width != (width - 1):
if costmap[lower_right] < lethal_cost:
step_cost = diagonal_step_cost + costmap[lower_right]/255
neighbors.append([lower_right, step_cost])
return neighbors
def dijkstra(start_index, goal_index, width, height, costmap, resolution, origin, grid_viz = None):
'''
Performs Dijkstra's shortes path algorithm search on a costmap with a given start and goal node
'''
#Task 1
#### To-do: complete all exercises below ####
open_list = [] # open_list: an empty list that will store open nodes as a sublist using this format: [index, g_cost]
#closed_list = []# closed_list: an empty set to keep track of already visited/closed nodes
closed_list = set() # They used set function because the order of the visited nodes does not matter in this list. And set store the elements in the list unordered
parents = {} #parents: a blank dictionary for mapping children nodes to parents .
g_costs = {} #g_costs : a dictionary where the key corresponds to a node index and the value is the associated g_cost.
start_index_dic = {"start_index":0} # Set the start's node g_cost: update g_costs using start_index as key and 0 as the value (as the travel distance to itself is 0.
g_costs.update(start_index_dic)
#Put start_index along with it's g_cost into open_list
open_list.append(g_costs) #open_list.append(g_costs["start_index"]) # if you wish just the value use the commented code line
#We do this because we want to be able to sort all nodes inside open_list by their lowest g_cost value later
shortest_path = [] # To conclude this exercise, create shortest_path as another empty list that we will use to hold the result of the search
path_found = False # Finally, create the variable name path_found and assign False to it. We will use this boolean flag later on to know if the goal was found or the goal was not reachable.
rospy.loginfo(' Dijkstra: Initialization done!') # If you want, you can finish the initialization step with a message on the console using this syntax:
#return shortest_path #Also, if you want to test your code for any errors, replace the pass statement and make the function return the empty list shortest_path.
#pass
# Task2: let's add some of the core functionality of Dijkstra, and begin implementing the main loop.
# create a loop that executes as long as there are still nodes inside open_list
while len(open_list) != []:
#Now we want to select the node with the lowest g_cost as current node
open_list.sort(key = lambda x: x[1]) # sort open_list in order to get the nodes ordered by the lowest 'g_cost' value
#The code above change the key for the node name index stored in [0] to its value stored in [1] as the new key. The sort function will put them in open list in increasing order.
current_node = open_list.pop(0)[0] # get the first element of open_list and call it current_node. The code open_list.pop(0) will extract both key (node_index) and (value) then it is necessary to add [0] to get just the node_index and not its value as desired
#closed_list.append(current_node) # add current_node into closed_list
closed_list.add(current_node) # It is the same of the cmd above but now closed_list is "set" type, which requires add cmd
grid_viz.set_color(current_node, "pale yellow")
if current_node == goal_index: # add a conditional statement to exit the main loop if the goal node has been reached
path_found = True
break
# I will comment the line below, because They did not use on solution, besides they have said to add...
#g = current_node[1] # get the g_cost corresponding to current_node and assign it to a variable named 'g'
#find_neighbours() # call the provided function find_neighbours()
#neighbours = find_neighbors() # and save the result into a variable named 'neighbours'
neighbours = find_neighbors(current_node, width, height, costmap, resolution) # I forgot to add the args previously,
#without args the fucntion will not work, once it is necessary to know "who/where" the current_node is to get neighbors, as well as the grid size allowed to visit/expand
#Task 3 - The loop needs to be inner the other loop to get different g_cost values for the new current_node values, as the open_list is swept
#Invoke a loop over all elements in neighbours
neighbours_iterator = iter(neighbours) # Created this to have the possibility to skip a specific neighbour index of a list as required below
for element in neighbours_iterator:
#Unpack each neighbor into neighbor_index and step_cost for later use
neighbor_index = element[0]
step_cost = element[1]
#Check if neighbor_index is in closed_list, and if so, skip the current loop iteration and proceed with the next neighbour
if neighbor_index in closed_list:
neighbours_iterator.next() # is it necessary
continue # I am not sure if this will work or is needed another statement, and where the next identations should be
#Next, determine the cost of travelling to the neighbor. We need it for the subsequent steps. Name g_cost the travel cost required to get to current_node plus step_cost (the cost of moving to the neighbor).
#g_cost = g + step_cost # I think it is wron because will always get hte cost of g the old current_node out of the loop
g_cost = g_costs[current_node] + step_cost
# Now verify if neighbor_index is currently part of open_list. If found, keep track of the position where the [index, g_cost] element appears as you will need it to update it as described in Case 1 below:
#in_open_list = False # I forgot to add this check line, so copied from solution
if neighbor_index in open_list:
# Case 1:if the neighbor is already inside open_list: Verify that g_cost is better than the neighbor's current g_cost value, if so:
neighbor_new_cost = g_cost
neighbor_current_cost_open_list = [sub[neighbor_index] for sub in open_list]
# If so Update the node's g_cost inside g_costs
if neighbor_new_cost < neighbor_current_cost_open_list:
g_costs.update({neighbor_index:neighbor_new_cost})
#Modify its parent node, set it to current_node
parents.update({neighbor_index:current_node}) # It is the same as the else statement? Strange...
#Update the node's g_cost inside open_list
open_list.clear() # It is not necessary once the value of key updated above in dictionary will automatically update the list too
open_list.append(g_costs)
#Case 2, if the neighbor is not part of open_list: # It is not said but I believe it must be added not just the neighbor but also its value as well, then I will use "element" that contains both
else:
#Set the node's g_cost inside g_costs
g_costs.append({neighbor_index:g_cost}) # There is not verification as previously, you need just the step to add
#Set current_node as its parent node
parents.update({neighbor_index:current_node}) # Using update will let the first neighbor and its corresponding parent
#at the end of the parents_dictionary after finish the search, that is why it is needed to reverse the order later.
#Another issue that I realize now, is that the for loop needs to be inside the while loop, otherwise the "current_node" will always be the same.
#This is critical code considering it will have a lot of loops inside another and will become too slow, I believe
#Add the neighbor into open_list
open_list.append(element)
#Optional: add this line of code to visualize the frontier:
grid_viz.set_color(neighbor_index,'orange')
rospy.loginfo('Dijikstra: Done traversing nodes in open_list')
# Final Task: Reconstruction of the shortest path
#if current_node != goal_index: #Out the for loop the current_node will be the last element of search, then must be the goal_index
#or you should be able to use also the last closed_list array element =
if closed_list[-1] != goal_index:
rospy.logwarn( 'Djikstra: No path found!')
else:
node = goal_index # Declare a variable named node and assign the target node to it
#Enter a loop that keeps going until 'node' is equal to start_index
while node != start_index: #At each iteration step:
#for node in parents:
# while node != start_index:
# Append node to shortest_path
# shortest_path.append(node)
# Get the next node by re-assigning node to be the node's parent node
shortest_path.append(node)
# Copy from solution below, however I do not understand how the node iterates over the parents dictionary
# withou a for loop over parents. How does it go to next node?
node = parents[node]
shortest_path.reverse() #Once the loop exits, reverse shortest_path to get the correct order
ropsy.loginfo('Dijkstra: Done reconstructing path')
return shortest_path
Well I am just curious if my code is able to work changing a little bit the logic, but this question is not so much important if you do not have much available time…I will understand.
And another assumption and question is:
It was a lot of time comsumption to understand this algorithm and implement it. The other 2 lectures about A* search algorithm and RRT have similar context (open list, closed, list, neighbours, etc). Or is it also very high demanding time to learn (From 0, totally new concept)??
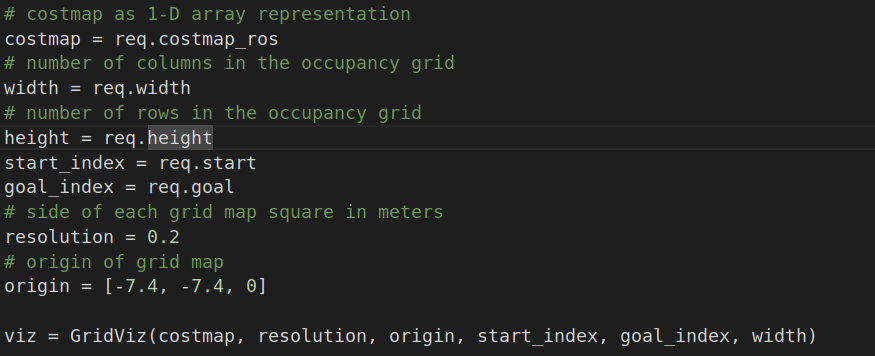
A complementar question, is regarding the “unit2_exercise_server.py”. The required service client and service server for the path planner be called…
Looking into the server and also into the Djikstra algorithm function in unit2_exercise.py script:
- I did not find where the following parameters are passed:
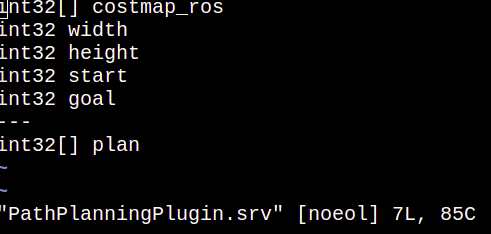
As well as asked in the beginning of this question, about the logic of the neighbours. It is not assigned there the size of the squares to be put inside the path list (response of service), right?
And finally the last question is regarding the line that the service make plan is called ( I forgot a little bit of services)
the “make_plan” is a the name of a created service previously? I tried to use “roscd” to locate it on RIA to understand from where it comes and goes.
This make plan create the response of the service defined in “PathPlanningPlugin” (which is the path list) ?
Or does it call a client to request the map width, height and parameters?
Where are these parameters informed? (In Alberto Ezquerro live class on youtube it was assumed the size 1, but here I do not see where this value is given).
I would like to understand better this server.py script, can I find some code explanation somewhere?